图形程序中最通用的工具或许是对点和矢量进行改变或转换的矩阵。在下一章中，我们将了解如何用单列矩阵表示向量，以及如何通过与方阵相乘以便在不同的基来表示向量。我们还将介绍如何利用这种乘法来实现向量的缩放、旋转和平移等变化。在本章中，我们将在二维和三维的场景中，通过直觉及算法来从几何的角度回顾基本线性代数。

如果读者对线性代数比较熟悉，可以跳过本章。不过，即使对这类读者来说，也会有一些启发性的小知识，例如行列式的发展以及奇异值和特征值分解的讨论。

6.1 行列式

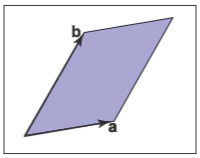
我们通常使用行列式来解线性方程。此外，从图形学方面来看，我们还可以把行列式看作多维向量的另一种形式。对二维向量$\boldsymbol{a}$和$\boldsymbol{b}$，行列式$|\boldsymbol{ab}|$的就是这两个向量形成的面积（图6.1）。这个面积是有符号的，如果是右手系，则结果为正；左手系结果为负。也就是$|\boldsymbol{ab}| = -|\boldsymbol{ba}|$。在2D中，我们说的“右手系”是指第一个向量沿逆时针旋转最少的角度就可以与第二个向量重合。

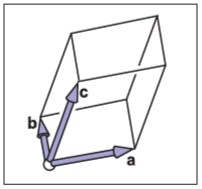
在三维空间中，行列式是由三个向量组成的，三维向量$\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{c}$组成的行列式$|\boldsymbol{abc}|$是一个由这三个向量组成的平行六面体（图6.2）。

为了计算二维行列式，我们需要首先了解一些性质。

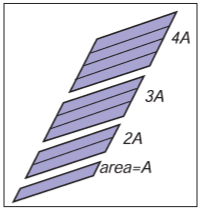
当我们缩放其中一个向量，平行四边形的面积也随之缩放同样的倍数（图6.3）：

$$ |(k\boldsymbol{a})\boldsymbol{b}| = |\boldsymbol{a}(k\boldsymbol{b})| = k|\boldsymbol{ab}| $$

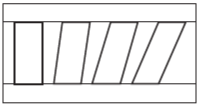
同样，我们对平行四边形进行剪切变换，也不会改变其面积（图6.4）：

$$ |(\boldsymbol{a}+k\boldsymbol{b})\boldsymbol{b}| = |\boldsymbol{a}(\boldsymbol{b}+k\boldsymbol{a})| = |\boldsymbol{ab}| $$

此外，行列式还有以下属性：

$$ |\boldsymbol{a}(\boldsymbol{b}+\boldsymbol{c})| = |\boldsymbol{ab}| + |\boldsymbol{ac}| $$

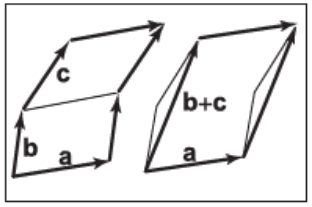
如图6.5所示，我们可以在不改变面积的情况下，把两个平行四边形的边进行滑动，形成一个大的平行四边形。

假设有笛卡尔坐标系下的两个向量$\boldsymbol{a}$和$\boldsymbol{b}$，则：

$$ \begin{eqnarray} |\boldsymbol{ab}| & = & |(x_a\boldsymbol{x} + y_a\boldsymbol{y} )(x_b\boldsymbol{x} + y_b\boldsymbol{y})| \\ ~ & = & x_ax_b|\boldsymbol{xx}| + x_ay_b|\boldsymbol{xy}| + y_ax_b|\boldsymbol{yx}| + y_ay_b|\boldsymbol{yy}| \\ ~ & = & x_ax_b(0) + x_ay_b(+1) + y_ax_b(-1) + y_ay_b(0) \\ ~ & = & x_ay_b - y_ax_b. \end{eqnarray} $$

化简的时候用到了一个性质：对于任意的向量$\boldsymbol{v}$，都有$|\boldsymbol{vv}|=0$。因为共线的两个向量组成的平行四边形的面积为0。

在三维情况中，三维向量 $\boldsymbol{a}$ 、 $\boldsymbol{b}$ 、 $\boldsymbol{c}$ 的行列式用 $|\boldsymbol{abc}|$ 表示。同2D情况一样，我们可以将其展开为：

$$ \begin{eqnarray} |\boldsymbol{abc}| & = & |(x_a\boldsymbol{x} + y_a\boldsymbol{y} + z_a\boldsymbol{z})(x_b\boldsymbol{x} + y_b\boldsymbol{y} + z_b\boldsymbol{z})(x_c\boldsymbol{x} + y_c\boldsymbol{y} + z_c\boldsymbol{z})| \\ ~ & = & x_ay_bz_c - x_az_by_c - y_ax_bz_c + y_az_bx_c + z_ax_by_c - z_ay_bx_c. \end{eqnarray} $$

显然，随着维数的增加，以这种方式来计算行列式会变得越来越难看。我们将在第 6.3 节讨论怎样在计算行列式的时候更不容易出错。

例2 在计算一个由另外两个向量的线性组合而得到的向量时，行列式便应运而生了。例如，如果我们用向量$\boldsymbol{a}$和$\boldsymbol{b}$来表示向量$\boldsymbol{c}$，即：

$$ \boldsymbol{c} = a_c\boldsymbol{a} + b_c\boldsymbol{b} $$

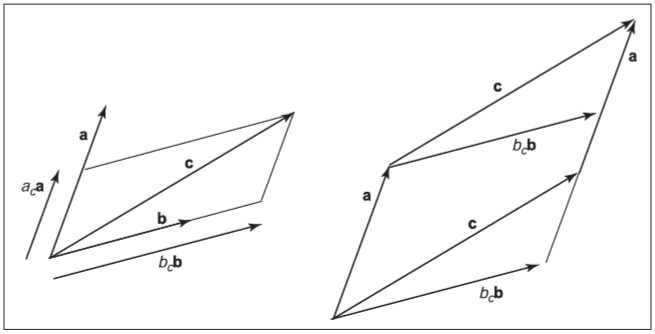
图6.6 左侧图中，向量 $\boldsymbol{c}$ 可以表示为 $a_c\boldsymbol{a} + b_c\boldsymbol{b}$ 。右侧图中，由向量 $\boldsymbol{a}$ 和 $\boldsymbol{c}$ 形成的平行四边形实际是剪切了的由 $b_c\boldsymbol{b}$ 和 $\boldsymbol{a}$ 形成的平行四边形。

由图6.6可得，下面等式两边所表示的平行四边形的面积是相等的：

$$ |(b_c\boldsymbol{b})\boldsymbol{a}| = |\boldsymbol{ca}| $$

可得$b_c$的值为：

$$ b_c = \frac {|\boldsymbol{ca}|}{|\boldsymbol{ba}|} $$

类似可得：

$$ a_c = \frac {|\boldsymbol{bc}|}{|\boldsymbol{ba}|} $$

这实际是二维版本的克莱姆法则。在6.3.2中我们会详细解释。

6.2 矩阵

矩阵是由数字元素组成的、遵循一定运算法则的数组。下面的数组有两行三列：

$$ \begin{bmatrix} 1.7 & -1.2 & 4.2 \\ 3.0 & 4.5 & -7.2 \\ \end{bmatrix} $$

矩阵在计算机图形学中有很多用处，如进行空间变换等。在讨论中， 我们假设矩阵的元素都是实数。本章会介绍矩阵的运算和方阵（即行数和列数相同的矩阵）对应的行列式。

6.2.1 Matrix Arithmetic 矩阵运算

一个矩阵和一个常数相乘，等于这个矩阵中每个元素与这个常数相乘，如：

$$ 2\left[\begin{matrix} 1 & -4 \\ 3 & 2 \end{matrix}\right] = \left[\begin{matrix} 2 & -8 \\ 6 & 4 \end{matrix}\right] $$

矩阵的加法就是矩阵的每个元素进行相加：

$$ \left[ \begin{matrix} 1 & -4 \\ 3 & 2 \end{matrix}\right]

• \left[\begin{matrix} 2 & 2 \\ 2 & 2 \end{matrix} \right] = \left[\begin{matrix} 3 & -2 \\ 5 & 4 \end{matrix}\right] $$

对矩阵乘法，我们将第一个矩阵的每一行与第二个矩阵的列进行“相乘”：

$$ \left[ \begin{matrix} a_{11}&\cdots& a_{1m} \\ \vdots&\ &\vdots \\ \hline a_{i1}&\cdots&a_{im} \\ \hline \vdots&\ &\vdots \\ a_{r1}&\cdots& a_{rm} \\ \end{matrix} \right] \left[ \begin{matrix} \begin{array}{cc|c|cc} b_{11}&\cdots& b_{1j} & \cdots & b_{1c} \\ \vdots & \ & \vdots & \ & \vdots \\ b_{m1} & \cdots & b_{mj} & \cdots & b_{mc} \\ \end{array} \end{matrix} \right]

\left[ \begin{matrix} p_{11} & \cdots & p_{1j} & \cdots&p_{1c} \\ \vdots & \ & \vdots & \ & \vdots \\ p_{i1} & \cdots& \boxed{p_{ij}} & \cdots & p_{ic} \\ \vdots & \ &\vdots & \ & \vdots \\ p_{r1} & \cdots & p_{rj} & \cdots & p_{rc} \\ \end{matrix} \right] $$

其中，元素$p_{ij}$的计算过程如下：

$$ p_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{im}b_{mj} $$

只有当左侧矩阵的列数等于右侧矩阵的行数时，才可以得到两个矩阵的乘积。例如：

$$ \left[ \begin{matrix} 0 & 1 \\ 2 & 3 \\ 4 & 5 \end{matrix} \right] \left[ \begin{matrix} 6 & 7 & 8 & 9 \\ 0 & 1 & 2 & 3 \end{matrix} \right] = \left[ \begin{matrix} 0 & 1 & 2 & 3 \\ 12 & 17 & 22 & 27 \\ 24 & 33 & 42 & 51 \end{matrix} \right] $$

在大多数情况下，矩阵乘法是不可交换的：

$$ \bold{AB} \neq \bold{BA} $$

同样，即使$\bold{AB} = \bold{AC}$，也不能导出$\bold{B} = \bold{C}$。但幸运的是，矩阵乘法是满足结合律和分配律的：

$$ (\bold{AB})\bold{C} = \bold{A}(\bold{BC}) \\ \bold{A}(\bold{B} + \bold{C}) = \bold{AB} + \bold{AC} \\ (\bold{A} + \bold{B})\bold{C} = \bold{AC} + \bold{BC} $$

TBD